Lambertian Surface

Wiki

Details Print

If a surface exhibits Lambertian reflectance, light falling on it is scattered such that the apparent brightness of the surface to an observer is the same regardless of the observer's angle of view. More technically, the surface luminance is isotropic.

The reflection is calculated by taking the dot product of the surface's normalized normal vector,

$\mathbf{N}$

, and a normalized light-direction vector,

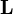
$\mathbf{L}$

, pointing from the surface to the light source. This number is then multiplied by the color of the surface and the intensity of the light hitting the surface:

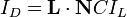$I_{D}=\mathbf{L}\cdot\mathbf{N} C I_{L}$ ,

where $I D$ is the intensity of the diffusely reflected light (surface brightness), $C$ is the color and $I L$ is the intensity of the incoming light. Because

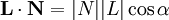$\mathbf{L}\cdot\mathbf{N}=|N||L|\cos{\alpha}$ ,

where $α$ is the angle between the direction of the two vectors, the intensity will be the highest if the normal vector points in the same direction as the light vector ( $cos(0) = 1$ , the surface will be perpendicular to the direction of the light), and the lowest if the normal vector is perpendicular to the light vector ( $cos(π / 2) = 0$ , the surface runs parallel with the direction of the light).

Lambertian reflection is typically accompanied by specular reflection, where the surface luminance is highest when the observer is situated at the perfect reflection direction, and falls off sharply.

Spectralon is a material which is designed to exhibit an almost perfect Lambertian reflectance, while Scotchlite is a material designed with the opposite intent of only reflecting light on one line of sight. ^[1]

References

[1] Wikipedia Page

15594 Views